本节内容主要为高精度运算、前缀和与差分的主要思想和代码。

高精度

基本思想

常考类型：

• $A+B$ ，两个的位数大约在 $10^6$ 。
• $A-B$ ，两个的位数大约在 $10^6$ 。
• $A\times a$ ， $A$ 位数大约 $10^6$ ，$a<10^9$ 。
• $A \div b$ ， $A$ 位数大约 $10^6$ ，$b<10^9$ 。

如何存储

使用数组进行存储，每一个位置存一个数，个位数存到开头（数组0位置）。

如何运算

竖式加减乘除，每一位是 $(A_i+B_i+t) \% 10$ ，其中 $t$ 为上一位运算的进位。

高精度加法

高精度加法使用 $t$ 来记录进位，当不超过 $A.size()$ 和 $B.size()$ 的时候继续计算
$$
C_i = (t+A_i+B_i)\%10，t = \frac{t+A_i+B_i}{10}
$$
需要注意的是循环完了可能还会进一位 $t$ ，所以要在结尾再判断一次。

核心函数：

vector<int> add(vector<int> &A, vector<int> &B){
    vector<int> C;
    int t = 0;
    for(int i = 0; i < A.size() || i < B.size();i++){
        if(i < A.size()) t += A[i];
        if(i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if(t) C.push_back(t);
    return C;
} 

此处使用引用类型，避免复制数组导致占用过多空间，下同

完整使用：

#include <iostream>
#include <vector>

using namespace std;

const int N = 1e6 + 10;

vector<int> add(vector<int> &A, vector<int> &B){
    vector<int> C;
    int t = 0;
    for(int i = 0; i < A.size() || i < B.size();i++){
        if(i < A.size()) t += A[i];
        if(i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if(t) C.push_back(t);
    return C;
} 

int main(){
    string a,b;
    vector<int> A,B;

    cin >> a >> b;
    for(int i = a.size() - 1; i>=0; i--){
        A.push_back(a[i] - '0');
    }
    for(int i = b.size() - 1; i>=0; i--){
        B.push_back(b[i] - '0');
    }
    auto C = add(A,B);
    for(int i = C.size() - 1;i>=0;i--){
        printf("%d",C[i]);
    }
    return 0;
}

高精度减法

步骤：

1. 判断 $A$ 和 $B$ 的大小：

• 如果 $A<B$ ，则 $return -jian(B,A)$ ；
• 如果 $A\ge B$ ，则正常计算。

1. 一位一位进行减法，设置一个大小为 $t$ 的变量记录借位，计算方法如下图：
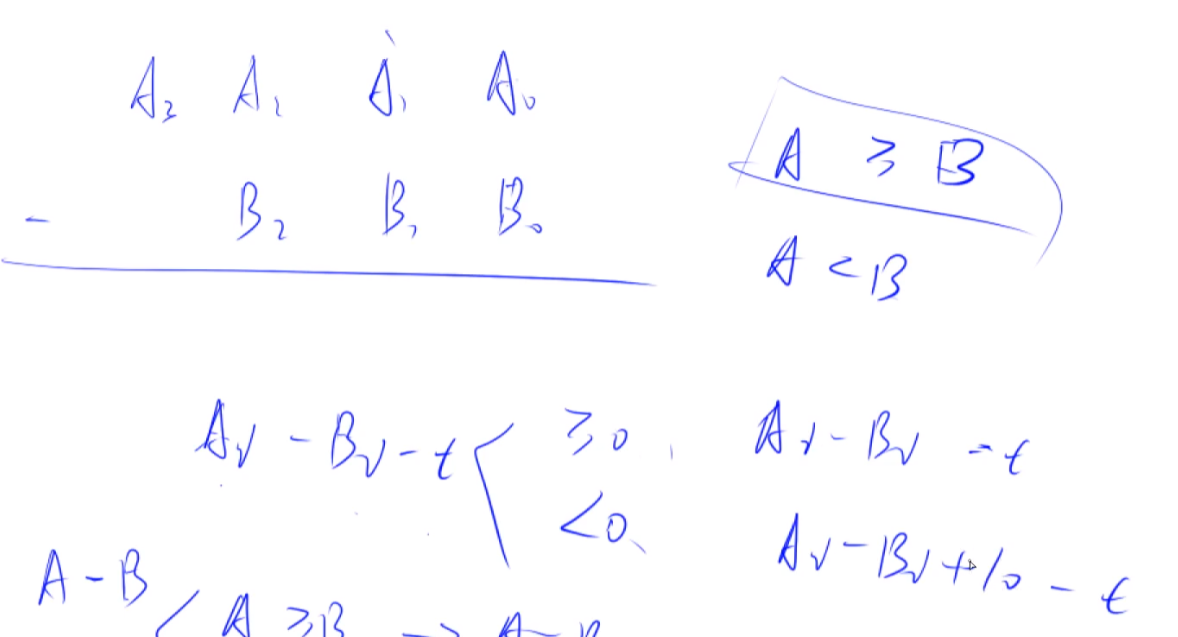
2. 判断得到的答案第一位是否会为0， 若为0则去掉一位，循环到第一位不是0或者只剩一位数且为0的情况。

代码

高精度比较大小：

bool cmp(vector<int> &A, vector<int> &B){
    if (A.size() != B.size()) return A.size() - B.size();
    for(int i = A.size() - 1; i >= 0 ; i--){
        if(A[i] != B[i]) return A[i] - B[i];
    }
    return true;
}

高精度减法：

vector<int> jian(vector<int> &A, vector<int> &B){
    vector<int> C;
    //if (cmp(A,B) == false) return jian(B,A); 此处无法加负号，要在外面判断限制
    int t = 0;
    for(int i = 0; i<A.size()||i<B.size(); i++){
        int w; // 用来存B[i]或者B的空位
        if(i>=B.size()) w = 0; 
        else w = B[i];
        if(A[i] - t >= w){ 
            C.push_back(A[i] - t - w);
            t = 0;
        }
        else {
            C.push_back(A[i] - w - t + 10);
            t = 1;
        }
    }
    while (C.size()>1 && C.back() == 0) C.pop_back();
    return C;
}

老师给的版本（优雅一些）：

// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ )
    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

高精度乘低精度

核心思想还是列竖式：对于乘法 $A\times b$ ，$A$ 的每一位计为 $a_i$ ，进位设为 $t$ 。则 $C_i = (a_i \times b + t) \% 10$ ，而 $t = \frac{a_i \times b + t}{10}$ 。

这个相对简单，没有什么需要额外考虑的，需注意循环条件要包括 $t > 0$ ，同样处理最后还有进位的情况。

vector<int> cheng(vector<int> &A, int b){
    vector<int> C;
    int t = 0;
    for(int i = 0; i < A.size() || t > 0;i++){
        if(i < A.size()) t += A[i] * b;
        C.push_back(t%10);
        t = t/10;
    }
    return C;
}

高精度除以低精度

还是列竖式，但是除法是从最高位开始看的。所以初始 $i = A.size() - 1$ 。

对于除法 $A\div B$ ，$A$ 的每一位计为 $a_i$ ，上一位的退位设为 $r$ 。则 $C_i = \frac{r \times 10 + a_i}{b}$ ，$r = (r \times 10 + a_i)\%b$ 。

循环完得到的 $C$ 是反着的，所以要先用 #include <algorithm>里面的reverse(C.begin(), C.end())函数进行调转。此时也有可能存在同样的问题，即前面有前导零，所以需要删除所有的0，与减法一样。

也可以把余数输出出来，可以在参数里增加一个引用类型 int &r。

vector<int> chu(vector<int> &A, int b){
    vector<int> C;
    int r = 0;
    for(int i = A.size() - 1; i>=0; i--){
        r = r * 10 + A[i];
        C.push_back(r/b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

前缀和

一维前缀和

有一个长度为 $n$ 的数组，前缀和数组 $S_i = a_1 + a_2 + a_3 +…+a_i$ ，数组最好从下标1开始。定义 $a_0 = 0$ 以及 $S_0 = 0$ 。

如何求 $S_i$

递归，$S_i = S_{i-1} + a_i$

作用

求数组里一段数的和：比如求 $[l,r]$ 之间的数组和，直接使用 $S_r - S_{l-1}$ 降低时间复杂度。

示例题目

代码

#include <iostream>
using namespace std;

int n,m;
int arr[100009],s[100009];
int r,l;

int main(){
    cin >> n >> m;
    arr[0] = 0;
    s[0] = 0;
    for(int i = 1; i <= n; i++){
        cin >> arr[i];
        s[i] = s[i-1] + arr[i];
    }
    for(int i=0;i<m;i++){
        cin >> l >> r;
        cout << (s[r] - s[l-1]) << endl;
    }
}

提升cin效率： ios::sync_with_stdio(false);

二维前缀和

$S[i][j]$ 表示以$ (i, j) $为右下角的矩形区域的和。总体是容斥原理。

构造方法:$S[i][j] = A[i][j] + S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1]$

同样还是要设 S[0][j] = 0 和 S[i][0] = 0， S[i][j] 中 i 和 j 都从1开始计数。此时使用vector会方便一些，或者定义到全局数组。

使用方法：

查询子矩阵和，查询以$ (x_1, y_1) $为左上角、$(x_2, y_2) $为右下角的子矩阵和：

$sum = S[x_2][y_2]-S[x_1-1][y_2]-S[x_2][y_1-1]+S[x_1-1][y_1-1]$

差分

一维差分

对于数组 $a_1,a_2,…,a_n$ ，构造数组 $b_1,b_2,…,b_n$ ，使得 $a_i=b_1+b_2+…+b_i$，即让b数组是a的前缀和。

计算b数组：

$$
\begin{cases}
b_1 = a_1 \
b_i = a_i - a_{i-1}
\end{cases}
$$

使用方法

由 $O(n)$ 可以由$b$推出$a$。

若需要对$a$数组的 $[l,r]$ 区间上每一个数都加上常数$c$，只需给 $b_l + c$ 并给 $b_{r+1} - c$ 。此时给$a$数组连续区间全部添加上或者减去一个常数，只需要改变差分数组的两个数，此时时间复杂度只有 $O(1)$ 。

可以开始把所有 $a_i$ 都看为0，然后调用连续区间加常数的函数用来初始化赋值，这样只需要定义一个函数。

void insert(int*b,int l,int r,int c){
    b[l] += c;
    b[r+1] -= c;
    return;
}

代码

#include <iostream>
using namespace std;

int n,m;
int arr[100009],b[100009];
int r,l,c;

void insert(int*b,int l,int r,int c){
    b[l] += c;
    b[r+1] -= c;
    return;
}

int main(){
    cin >> n >> m;
    arr[0] = 0;
    b[0] = 0;
    for(int i = 1; i <= n; i++){
        scanf("%d",&arr[i]);
    }
    for(int i = 1; i <= n; i++){
        insert(b,i,i,arr[i]);
    }
    while(m--){
        int l,r,c;
        scanf("%d%d%d",&l,&r,&c);
        insert(b,l,r,c);
    }
    for(int i = 1 ; i <= n; i++){
        printf("%d ",b[i]);
    }
}

二维差分

有一个原矩阵 $a_{ij}$ ，构造差分矩阵 $b_{ij}$ ，使$a$是$b$的前缀和。

若想将 $(x_1,y_1)$ 到 $(x_2,y_2)$ 范围内所有数加 $c$ ，需要进行以下操作：
$$
\begin{cases}
b_{x_1,y_1} + c \
b_{x_2+1,y1} - c \
b_{x_1, y_2+1} - c \
b_{x_2+1,y_2+1} + c
\end{cases}
$$
改变这四个值即可。