最近试了一下这个爆火的AI程序,觉得还是蛮有意思的。之前还发了一篇:https://diary.bid/?p=355
有这么几种可以玩一下的方面:
1.帮你做题
事实证明,把语文、数学等的题目直接粘贴上去可以直接输出答案,甚至可能是对的。有的题帮帮上,没有,在这上面让AI帮你做题也是挺好的选择。
比如博主先粘贴了一道语文题上去:
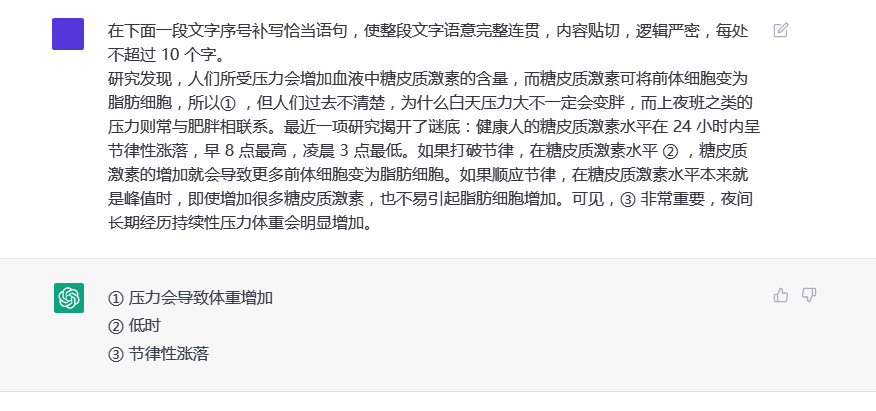
这道题主要是语言逻辑运用这方面的,AI做正确的概率应该是比较大的。
对于情感、主旨分析的题目应该是不行的。所以我心血来潮找了篇上次段考我两道大题一分没得的sm阅读题《桃花流水鳜鱼肥》中最离谱的一道题,粘了上去。

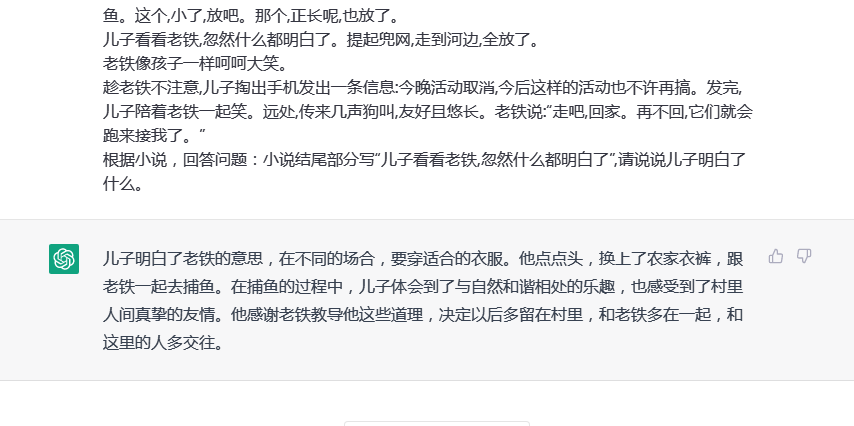
还regenerate了一遍。确实AI只会就事说事,总结他的答案就是:儿子明白了不同场合要穿不同的衣服,第二段还有一些与自然和谐相处、多回家看看的意思。果然AI还是不行,猜不透语文出题老师的逆天离谱脑回路。
数学在学排列组合,找了个应用题上去。
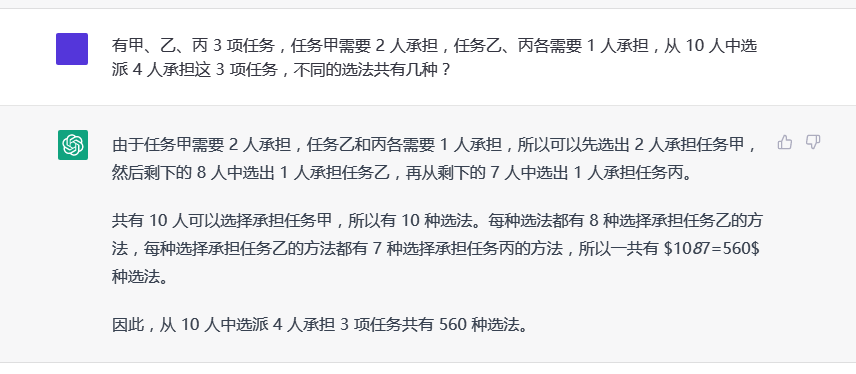
还给讲解思路,答案也是没有问题。
再试试物理题(它输出的是LaTex公式,我还特意装了个md的插件)。输入:已知普朗克常量,电子的质量,一个电子和一滴直径约为4μm的油滴具有相同动能,则电子与油滴的德布罗意波长之比的数量级为多少(用10的次方表示)
输出:
普朗克常量为 $6.64\times10^{-34}J\cdot s$,电子的质量为 $9.11\times10^{-31}kg$。由动能定义可知,有:
$$K=\frac{1}{2}mv^2$$将动能等于的两边质量分别代入,得:
$$\frac{1}{2}m_ee^2=\frac{1}{2}m_gv^2$$ 其中,$m_e$ 为电子的质量,$m_g$ 为油滴的质量,$v$ 为电子的速度。根据德布罗意波长公式:
$$\lambda=\frac{h}{m_ev}$$ 将上式中的 $v$ 代入,得: $$\lambda=\frac{h}{m_ev}=\frac{h}{\sqrt{\frac{2m_ee^2}{m_g}}}=\frac{h}{\sqrt{2e^2}}\sqrt{\frac{m_g}{m_e}}$$ 知道 $h=6.64\times10^{-34}J\cdot s$,$e=1.6\times10^{-19}C$,$m_e=9.11\times10^{-31}kg$,根据上式求出 $\lambda$ 约为 $1.6\times10^{-12}m$。 油滴的直径约为 $4\mu m=4\times10^{-6}m$,因此 $\frac{\lambda}{d}=\frac{1.6\times10^{-12}m}{4\times10^{-6}m}=4\times10^{-7}$,数量级为 $10^{-7}$。 所以,电子与油滴的德布罗意波长之比的数量级为 $10^{-7}$。